A turbulens spektrum időbeli változásának modellezése DNS eredmények felhasználásával / Modeling the Temporal Variation of a Turbulence Spectrum Using DNS Results
Az időátlagolt áramlásban jelenlévő deformációsebesség (nyírás) random sebességingadozás formájában turbulens mozgási energiát „produkál”. A turbulnecia állapotát legjobban a turbulens energiaspektrummal jellemezhetjük, mely megmutatja a mozgási energia eloszlását a hullámszám függvényében. A nyírás okozta turbulens produkció egy meghatározható, keskeny hullámszám tartományban energiát juttat a spektrumba, mely a hullámszámtérben a növekvő hullámszámok irányában „áramlik” tovább. Eközben a viszkózus erők okozta disszipáció hatása egyre növekszik, ami korlátot szab a legkisebb örvények méretének (Kolmogorov-féle hosszlépték). E folyamat a Kolmogorov-egyenlet alkalmazásával nagy pontossággal leírható, a jelenleg alkalmazott turbulencia modellek azonban mégsem használják ki a spektrum előrejelzésének lehetőségét. Feltehetőleg a spektrum tárolásához szükséges adatmennyiség korlátozta a módszer elterjedését a modern áramlásmodellekben. Ezt a problémát azonban áthidalhatjuk úgy, hogy a turbulens spektrumot nem minden numerikus cellában tároljuk, hanem csupán az áramlással együtt mozgó (súlytalan) részecskék pályája mentén állítjuk elő, melyhez a modern CFD eszközök, így például az ANSYS Fluent vagy az OpenFOAM kiváló alapot ad.
Célunk, a mérnöki gyakorlatban elterjedt, klasszikus Reynolds-átlagolt áramlásmodellekhez (például k-omega SST modellhez) kapcsolható spektrális turbulenciamodell előállítása, mely a korábbi módszereknél pontosabb adatokat szolgáltathat például a turbulens zajról és a turbulencia okozta szerkezeti rezgésekről. További cél lehet a Reynolds-átlagolt modellek továbbfejlesztése a spektrális modellből nyert adatok segítségével.
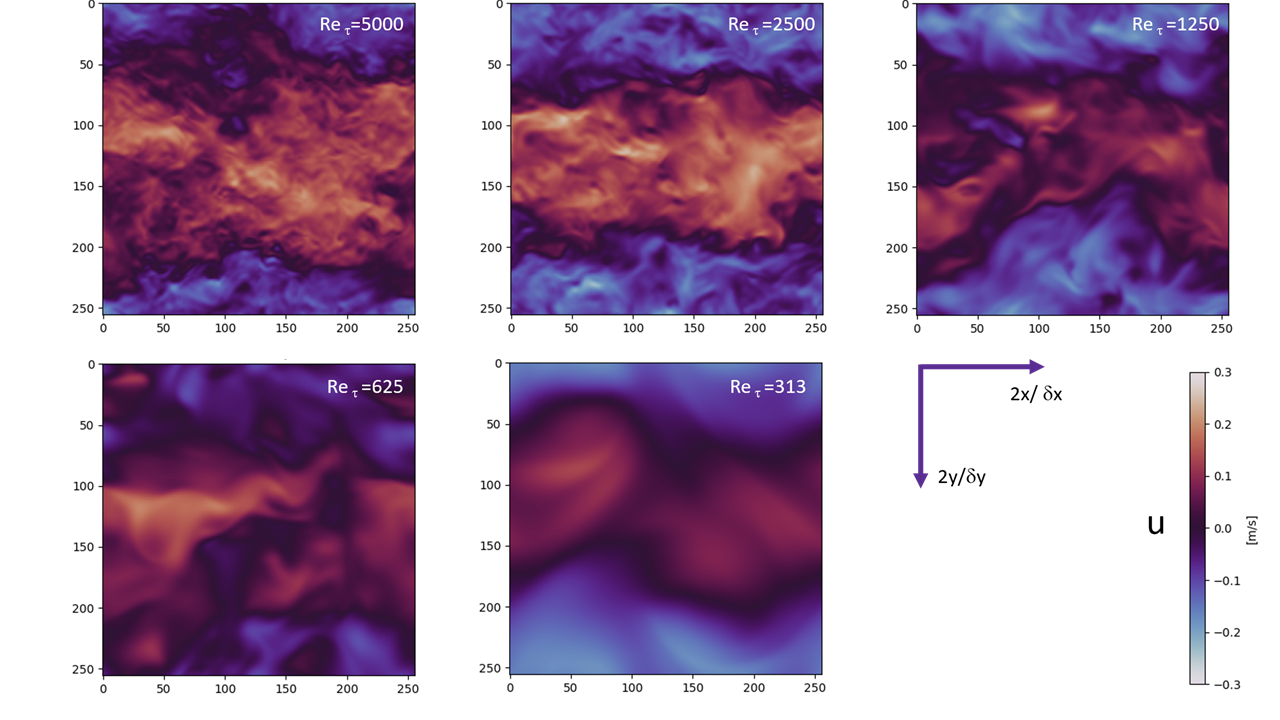
A feladat megoldásához nyilvánosan elérhető Direkt Numerikus Szimuláció (DNS) adatbázisokat, valamint különféle (akár időben változó) nyírásokkal gerjesztett turbulenciára vonatkozó saját DNS adatokat tudunk fölhasználni. Például, a mellékelt ábrán – különféle Reynolds-szám mellett – állandó nyírással gerjesztett turbulens áramlások áramképe látható.
A feladatot TDK-ként, szakdolgozatként vagy diplomaterv feladatként ajánlom megkezdeni, e mellett akár PhD kutatási témaként is folytatható egy folyamatban lévő NKFIH alapkutatási projekt (OTKA) keretében.
Szükséges előismeretek: a Python alapszintű ismerete, CFD („Áramlások numerikus modellezése” c. BSc tantárgy).
Dr. Kristóf Gergely
The deformation velocity (shear) present in the time-averaged flow produces turbulent kinetic energy in the form of random velocity fluctuations. The state of turbulence is best characterized by the turbulent energy spectrum, which shows the distribution of kinetic energy as a function of wavenumber. Turbulent production caused by shear injects energy into the spectrum in a specific, narrow wavenumber range, which then ‘flows’ further in the wavenumber space towards increasing wavenumbers. Meanwhile, the effect of viscous forces causing dissipation increases, which limits the size of the smallest eddies (Kolmogorov microscale). This process can be described with high accuracy using the Kolmogorov equation, but current turbulence models do not yet exploit the potential of spectrum prediction. Presumably, the amount of data required to store the spectrum limited its widespread adoption in modern CFD models. However, this problem can be overcome by not storing the turbulent spectrum in every numerical cell, but rather generating it along the path of weightless particles moving with the flow, for which modern CFD tools, such as ANSYS Fluent or OpenFOAM, provide an excellent foundation.
Our goal is to develop a spectral turbulence model that can be linked to the classic Reynolds-averaged flow models (such as the k-omega SST model) commonly used in engineering practice, which can provide more accurate data, for example, about turbulent noise and structure-induced vibrations caused by turbulence. Another goal might be the further development of Reynolds-averaged models with the help of data derived from the spectral model.
To solve the task, we can use publicly available Direct Numerical Simulation (DNS) databases, as well as our own DNS data related to turbulence excited by various (possibly time-varying) shears. For example, the attached image shows the flow patterns of turbulent flows excited by constant shear at various Reynolds numbers.
I recommend undertaking this task as a topic for a Scientific Students’ Associations Conference (TDK), a bachelor’s thesis, or a diploma project. Additionally, it can be pursued as a PhD research topic within the framework of an ongoing NKFIH basic research project (OTKA).
Required preliminary knowledge: Basic knowledge of Python, CFD (Numerical Modelling of Flows – a BSc course).
Dr. Gergely Kristóf